Scipyでベータ分布を扱う

もんた

scipyは、科学技術計算のためのPythonライブラリで、確率論や統計学に関連する多数の関数が提供されています。その中で、beta分布に関連する関数をメモしておきます。

beta.pdfの使い方

beta.pdfは、beta分布の確率密度関数を表す関数です。beta分布は、0から1の範囲で値を取る連続的な確率分布で、2つのパラメータaとbによって形状が決定されます。この関数を使うことで、特定のパラメータに対応する確率密度関数をプロットできます。

引数の説明

beta.pdfは以下の引数を取り、確率変数の値がxである確率密度を返します。

scipy.stats.beta.pdf(x, a, b, loc=0, scale=1)

• x: 確率変数の値を指定するための引数です。xは実数値か、またはNumPyの配列で指定できます。
• aとb: ベータ分布のパラメータを指定するための引数です。aとbはいずれも非負の実数値で、共に0以上でなければなりません。
• loc: 分布の平均を指定するための引数です。デフォルト値は0です。
• scale: 分布の標準偏差を指定するための引数です。デフォルト値は1です。

beta分布をプロット

import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt

a, b = 2, 3
x = np.linspace(0, 1, 100)
y = beta.pdf(x, a, b)

plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('Probability density')
plt.title('Beta distribution with a=2, b=3')
plt.show()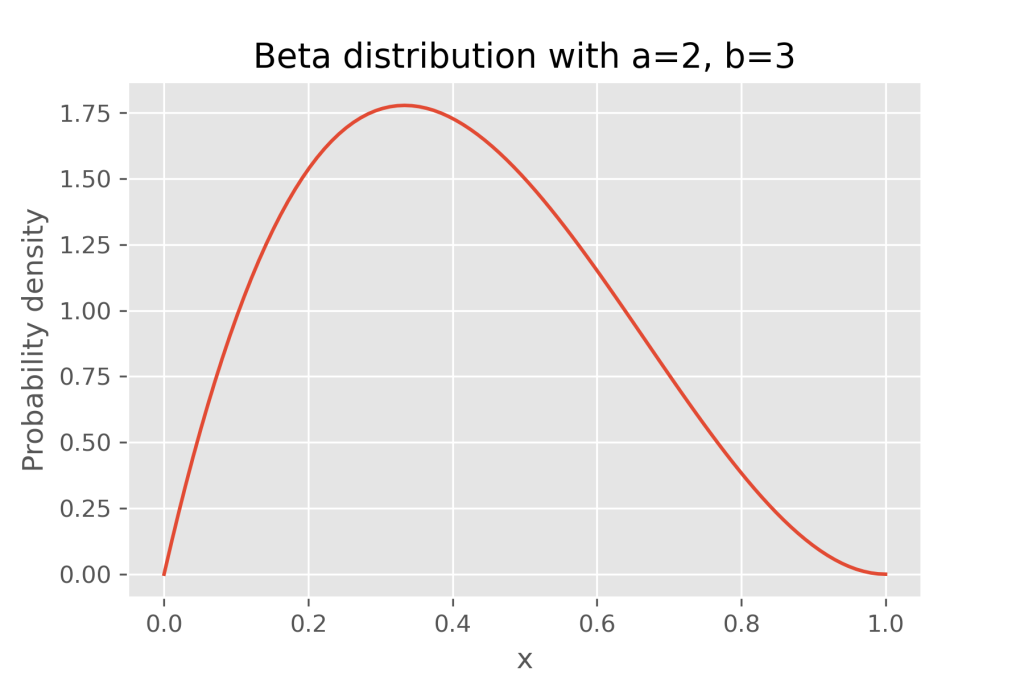

beta分布の累積分布関数はbeta.cdfを使う

beta.cdf(x, a, b)は、beta分布の累積分布関数（Cumulative Distribution Function; CDF）を計算する関数で、以下のように記述します。

a = 2
b = 3
x = 0.5

cdf = beta.cdf(x, a, b)
print(cdf) # 0.6875

• xは、確率変数が取りうる値。beta.cdf(x, a, b)は、確率変数がx以下になる確率を返します。
• aとbは、ベータ分布の形状パラメータ。

もんた

beta.cdf(x, 2, 3)の結果をプロットすると下図のようになります。

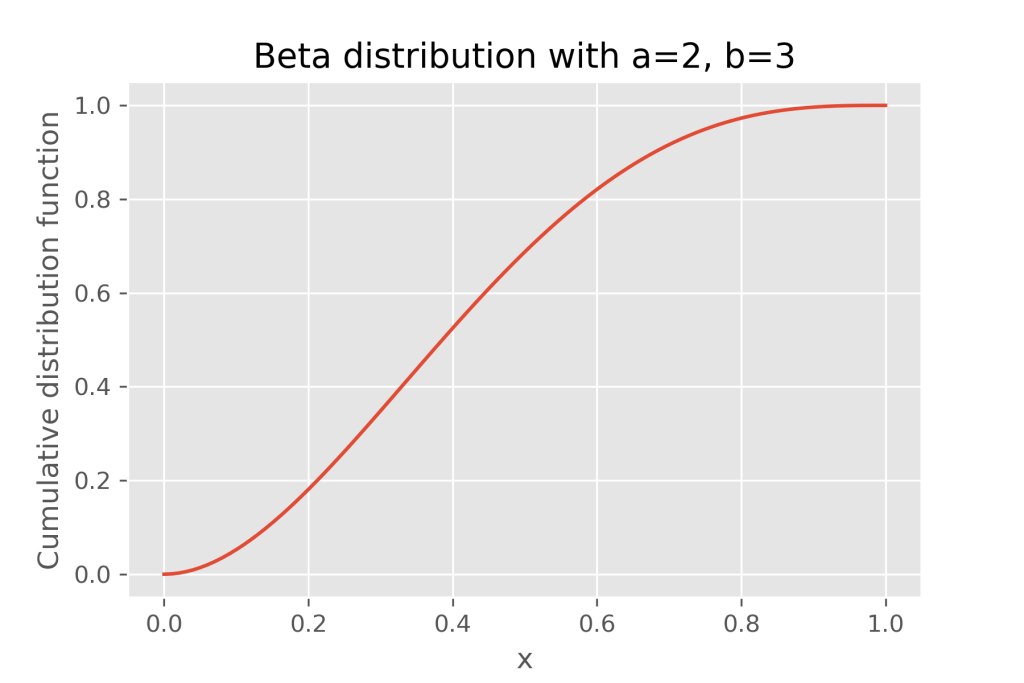
累積分布関数の逆関数はbeta.ppfを使う

beta.ppfは、累積分布関数の逆関数を表す関数で、以下を引数に取ります。

引数の説明

beta.ppf(q, a, b, loc=0, scale=1)

• q: 累積分布関数の値を指定するための引数です。qは実数値か、またはNumPyの配列で指定できます。qは0から1の間の値をとります。
• aとb: ベータ分布のパラメータを指定するための引数です。aとbはいずれも非負の実数値で、共に0以上でなければなりません。
• loc: 分布の平均を指定するための引数です。デフォルト値は0です。
• scale: 分布の標準偏差を指定するための引数です。デフォルト値は1です。

beta.ppfを使ってみる

beta.ppfは、beta分布の累積分布関数の逆関数を計算します。つまり、確率変数が何らかの値を取る確率が、qになるような確率変数の値を求めることができます。

from scipy.stats import beta

q = 0.5 # 累積分布関数の値
a = 2 # パラメータa
b = 3 # パラメータb

ppf_value = beta.ppf(q, a, b) # 累積分布関数の逆関数を計算
print(ppf_value)

このコードでは、累積分布関数の値qが0.7、パラメータaが2、パラメータbが3の場合のベータ分布の逆関数を計算しています。

もんた

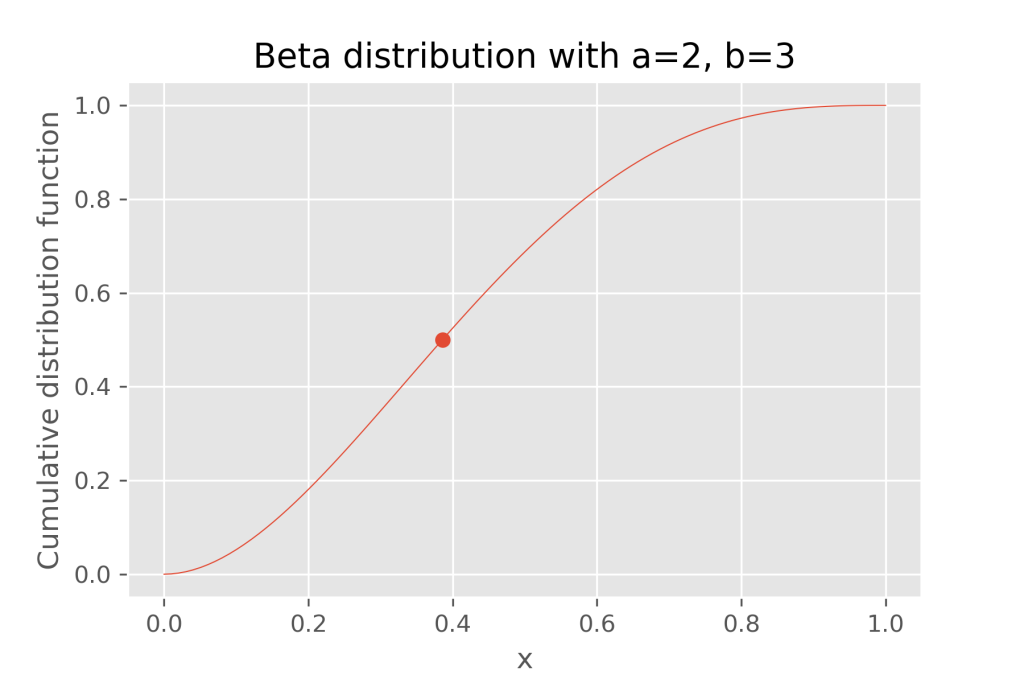
上のコードを実行すると、結果は0.385となります。求めた値を累積分布関数（上の例と同じ）と一緒にプロットすると、ちゃんと確率変数の値を逆算できていることがわかります。

# パラメータの設定
a = 2
b = 3

# x軸の値を用意
x = np.linspace(0, 1, 100)

# 累積分布関数を計算
cdf = beta.cdf(x, a, b)

# 累積分布関数の逆関数を計算
ppf_value = beta.ppf(q, a, b) 

# プロット
plt.plot(x, cdf, linewidth=0.5)
plt.scatter(ppf_value, 0.5)
plt.xlabel('x')
plt.ylabel('Cumulative distribution function')
plt.title('Beta distribution with a=2, b=3')
plt.show()