線形回帰モデルとは
線形回帰モデル(Linear Regression)とは、次のような回帰式により説明変数から目的変数の値を予想するモデルです。
$$ y = b_{0} + b_{1}x_{1} + b_{2}x_{2} + \cdots + b_{n}x_{n} + \varepsilon $$
ここで、\( x_{n} \)は説明変数、\( b_{n} \)は回帰係数、\( y \)は目的変数と呼ばれています。また、\( \varepsilon \)は観測された値との誤差です。説明変数が1つのとき、上記の式は直線の式として馴染み深い\( y = b + ax \)の形となりますが、これは「単回帰分析」と呼ばれています。
一方、説明変数が2つ以上で構成される場合を「重回帰分析」と呼びます。
例えば、年齢と年収のデータに対して、\( x \)を年齢、\( y \) を年収として回帰分析を行うと、年齢に応じて年収がどれだけ上下するか予測することができるようになります。
回帰分析をやってみる
ライブラリのインポート
まずは、分析に必要なライブラリをインポートします。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.linear_model import LinearRegressionデータの読み込み
まずは、上記のprice_dataを読み込みます。
data = pd.read_csv('price_data.csv')データの確認
読み込んだデータを確認します。今回は、データに欠損はないものとして扱っています。
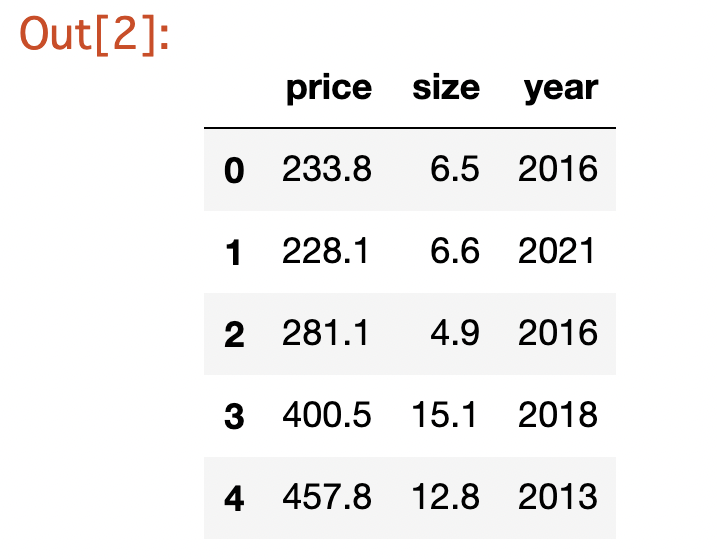
- ①はじめの5つのデータを確認する。
-
データの中身を確認するときには先頭5行を表示するheadメソッドが便利です。末尾の5行を表示するtailというメソッドもあります。
data.head()出力結果を見る - ②統計量を表示する。
-
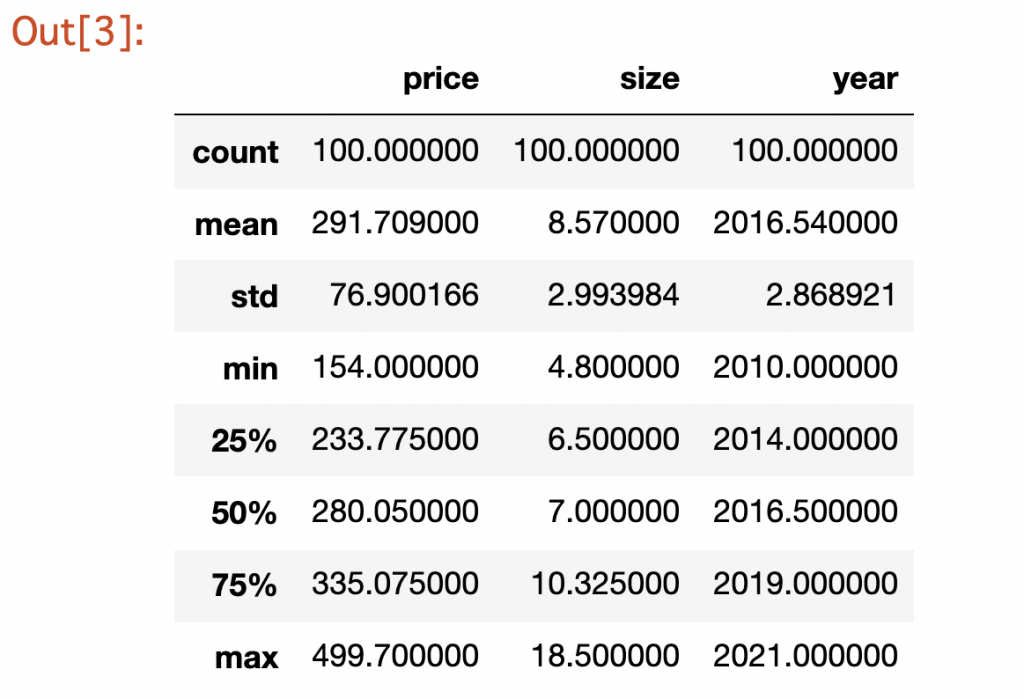
統計量を表示するためには、describeメソッドを使います。データの数や平均、標準偏差などが一覧で表示されます。
data.describe()出力結果を見る - ③グラフを書いてみる
-
ⅰ)2変数間の散布図の作成
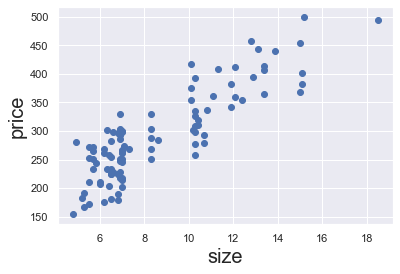
特定の2つのデータの関係を見たい場合は散布図が見やすいでしょう。散布図は、以下のコードで表示します。
# 散布図の作成 plt.scatter(data['size'],data['price']) # 軸に名前を付けておく plt.xlabel('size', fontsize = 20) plt.ylabel('price', fontsize = 20) plt.show()出力結果を見るⅱ)全てのデータの組み合わせを一括で散布図にする
 もんたたくさんある項目の関係性を一括で可視化したい場合は、ペアプロットがとても便利です。
もんたたくさんある項目の関係性を一括で可視化したい場合は、ペアプロットがとても便利です。sns.pairplot(data, vars = ['size', 'year', 'price'])出力結果を見る
回帰モデルの作成
説明変数と目的変数を定義する
データを読み込んで中身を眺めたら、いよいよ回帰モデルを作成します。まずは、各変数を定義していきます。
# 説明変数 'size' と 'year'を定義
x = data[['size','year']]
# 目的変数は 'price'を定義
y = data['price']回帰モデルを作成する
# クラスからオブジェクトを作成
reg = LinearRegression()
# モデルにフィットさせる
reg.fit(x,y)これだけで回帰モデルの作成は完了です。結果を出力してみましょう。
結果を表示する
上で述べた線形回帰式について、切片 \( b_{0} \) と係数 \( b_{1}, b_{2} \) が決まれば、回帰式が完成します。これらの係数、切片を表示させてみましょう。
# 係数の表示
reg.coef_
# 切片を表示
reg.intercept_上記を実行すると切片 \(b_{0}\)、sizeとyearの係数 \(b_{1}, b_{2}\) がぞれぞれ得られます。
reg.coef_ = 9136.49867349858
reg.intercept_ = array([22.49112242, -4.48170559])
特徴選択 ― 不要な変数を見つける
特徴選択
今回、sizeとyearからpriceの回帰モデルを作成しましたが、ここで各項目の関係をもう一度見てみます。下の図は、データの確認のところで見たペアプロットの出力結果です。この図をよく見ると、sizeとpriceには線形の関係がありそうですが、yearとpriceの間に関係性が見て取れません。
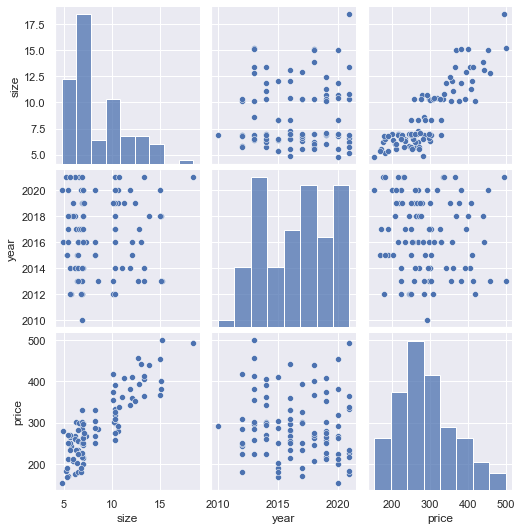
yearがpriceの予想に本当に必要な変数であったのか、確認してみましょう。もしyearがモデルの説明力を高めていないのであれば、削除してモデルをよりシンプルなものにしたほうが良さそうです。
f-regressionとは
変数が必要なものか確認する方法として、f-regressionというものがあります。これは、ひとつひとつの変数に対して、単線形回帰を行ってp値を算出します。
p値が0.05を超える変数は優位性がないと判断できるので、f-regressionの結果から不要な変数を判断することができます。f-regressionの方法は次のとおりです。
# f-regressionをインポートして実行
from sklearn.feature_selection import f_regression
f_regression(x,y)(array([286.44901672, 1.02812566]), array([7.59661299e-31, 3.13096173e-01]))
上記の出力結果で、左側(青)の配列はF値を、右側(オレンジ)の配列はp値を示しています。sizeのp値は非常に小さい値となっていますが、yearのp値は0.313であり0.05よりも高いため、不要と判断することができます。
未知のデータから結果を予測する
ということで、yearは重要な変数ではなかったので、変数から外してsizeだけの単回帰分析を行い、未知のデータを与えて結果を予想してみましょう。
単回帰分析
単回帰分析を行ってみます。重複した内容になるので、一気に見ていきましょう。
# 説明変数、目的変数を定義
x = data['size']
y = data['price']
# 単回帰分析の場合、reshapeを行う
x_matrix = x.values.reshape(-1,1)
# 回帰モデルを作成する
reg = LinearRegression()
reg.fit(x_matrix,y)
# 係数、切片の出力
reg.coef_
reg.intercept_
# 決定係数の出力
reg.score(x_matrix,y)reg.coef_ = array([22.17083826])
reg.intercept_ = 101.70491608352216
reg.score(x_matrix,y) = 0.7450897368999787
説明変数がsizeひとつだけの場合、決定係数は上記のように簡単に計算することができます。
結果を可視化してみる
結果を可視化してみましょう。各データを散布図上に表示し、回帰直線と合わせて表示してみます。
# データを散布図で表示
plt.scatter(x,y)
# 回帰式
y_hat = reg.coef_* x_matrix + reg.intercept_
# 回帰直線の表示
fig = plt.plot(x,y_hat, lw=3, c='orange', label ='regression line')
# 軸に名前をつける
plt.xlabel('size', fontsize = 20)
plt.ylabel('price', fontsize = 20)
plt.show()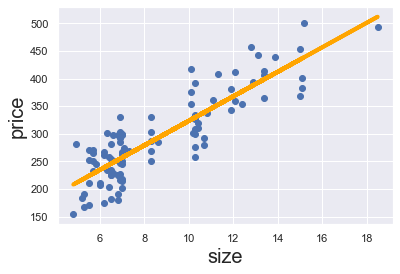
未知のデータから結果を予測
size=10のデータのpriceを予測してみましょう。予測にはpredictメソッドを使います。
reg.predict([[10]])array([323.41329872])
長きに渡って回帰分析を見てきましたが、とうとう未知のデータに対してpriceを予測することができました。この値は、上の回帰直線のsize=10のところにあることが見て取れるので、確認してみてください。