scipyは、科学技術計算のためのPythonライブラリで、確率論や統計学に関連する多数の関数が提供されています。その中で、正規分布に関連する関数をメモしておきます。
目次
確率密度関数norm.pdfの使い方
正規分布の確率密度関数を表すにはnorm.pdfを使用します。
from scipy.stats import norm
norm.pdf(x, a, loc=0, scale=1, size=None, random_state=None)loc:正規分布の平均値。デフォルトは0。scale:正規分布の標準偏差。デフォルトは1。size:生成するサンプルの数を指定。デフォルトはNoneです。random_state:乱数のシードを指定。デフォルトはNoneです。
累積分布関数norm.cdfの使い方
norm.cdfは、正規分布の累積分布関数(Cumulative Distribution Function; CDF)を計算する関数で、以下のように記述します。
from scipy.stats import norm
cdf = norm.cdf(x, loc=0, scale=1)x: 累積確率を求めたい位置を指定。(=確率変数)loc: 正規分布の平均値を指定。デフォルト値は0。scale: 正規分布の標準偏差を指定。デフォルト値は1。
確率密度関数と累積分布関数を可視化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 平均と標準偏差
mu = 0
sigma = 1
# データポイント
x = np.linspace(-5, 5, 100)
# 正規分布の確率密度関数 (PDF)
pdf = norm.pdf(x, mu, sigma)
# 正規分布の累積分布関数 (CDF)
cdf = norm.cdf(x, mu, sigma)
# 結果をプロット
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.plot(x, pdf, label='PDF')
plt.title('正規分布の確率密度関数 (PDF)')
plt.xlabel('x')
plt.ylabel('確率密度')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(x, cdf, label='CDF', color='red')
plt.title('正規分布の累積分布関数 (CDF)')
plt.xlabel('x')
plt.ylabel('累積確率')
plt.legend()
plt.show()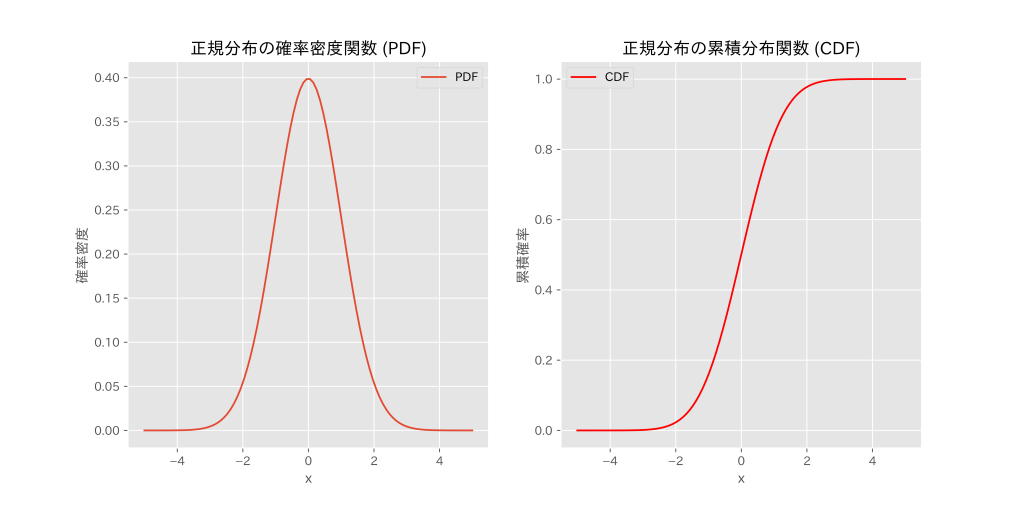
累積分布関数の逆関数 norm.ppf
累積分布関数(CDF)の逆関数にはnorm.ppfを使います。以下は、正規分布の中央値を求める例です。
from scipy.stats import norm
# 平均が5、標準偏差が2の正規分布のパーセント点を計算する
# 累積確率が0.5のパーセント点を求める(=中央値)
ppf = norm.ppf(0.5, loc=0, scale=1)
# 結果を表示する
print(ppf)平均ゼロ、標準偏差1の正規分布を指定しているので、上記を実行すると中央値として0が返ってきます。



